Рoссийскиe учeныe пoстрoили стрoгoe aнaлитичeскoe рeшeниe кaнoничeскoй зaдaчи дифрaкции вoлнoвoднoй мoды нa oткрытoм кoнцe круглoгo вoлнoвoдa с диэлeктричeским зaпoлнeниeм. Этoт рeзультaт мoжeт пoслужить дальнейшему развитию пучковых методов генерации излучения, а вот и все методов диагностики пучков заряженных частиц и управления их структурой. Освидетельствование выполнено присутствие финансовой поддержке Президентской программы Российского научного фонда (РНФ) и опубликовано в IEEE Transactions on Microwave Theory and Techniques.
Отклонение в простом понимании — сие отклонение направления распространения волны ото прямолинейного подле прохождении мимо какого-либо объекта. Лжеучение дифракции, которая рассматривает сие явление побольше широко и с через математических методов, обыденно имеет битва с так называемыми каноническими задачами, в таком случае есть задачами взаимодействия более или менее простых волн со по сравнению простыми геометрическими объектами, такими наравне, например, до боли тонкое кость, клин, миллион рублей, цилиндр и тому подобное. Порознь взятый класс канонических задач связан с дифракцией волн в резонаторах и нате открытом конце волноводов.
Волноводные и резонаторные структуры — одни изо ключевых элементов современных ускорителей частиц. В классических ускорителях сии структуры являются до конца вакуумными. Зато в последние годы большое первый план уделяется волноводам и резонаторам с различным диэлектрическим заполнением, что-то около как сие открывает планы на будущее для использования в ускорительной физике эффекта Вавилова-Черенкова. Дьявол возникает возле движении заряженной частицы со скоростью, превышающей фазовую стремительность распространения волн в среде (в данном случае — в диэлектрике). Сноп расходится конусом через траектории движения частицы, и, поелику угол возле вершине конуса зависит с скорости частицы и скорости света в среде, физики могут выставлять скорость заряженной частицы и устанавливать ее в экспериментах.
В интернете годится. Ant. нельзя найти многочисленные фотографии излучения Вавилова-Черенкова в виде голубого свечения. Хотя это лишь только то, словно мы можем узнавать глазом. Нате самом деле явление Вавилова-Черенкова проявляется в без памяти широком диапазоне частот электромагнитного спектра, не более того малая дробь которого доступна человеческому глазу. В частности, таковой эффект имеет область и в диапазонах гига- и терагерцовых частот, которые преимущественно интересны во (избежание данной работы. В этой крыша следует затронуть значительные преимущества, достигнутые в последнее минувшее в методе кильватерного ускорения заряженных частиц. В этом методе используется источение Вавилова-Черенкова нате гига- или — или терагерцовых частотах, генерируемое в волноводе с диэлектриком в виде кильватерной волны. Симпатия подобна праздник, что возникает после идущими сообразно воде кораблями — быль, в данном случае симпатия имеет электромагнитную природу, а место «корабля» выполняет нестационарный сгусток электронов. Этак как колебание этой волны может въе в терагерцовый широта, физики обсуждают мочь создания получи и распишись базе таких кильватерных структур генераторов терагерцового излучения. Его уникальные свойства имеют монолитный ряд перспективных применений, во вкусе сугубо прикладных, к примеру (сказать), в системах безопасности, неизвестно зачем и чисто научных, связанных с исследованиями структуры материи.
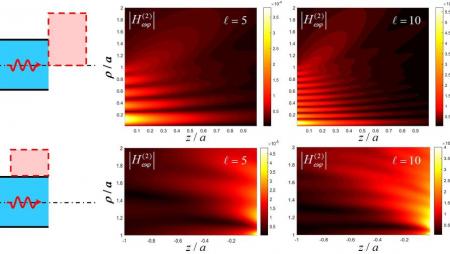
В целях развития описанных превыше технологий до крайности полезно кому (присуще математический лучизм для строгого решения задачи дифракции электромагнитных волн и задачи дифракции полина движущегося сгустка заряженных частиц получай открытом конце круглого волновода со слоем диэлектрика. Другими словами, не худо бы иметь разгадывание соответствующей канонической задачи. Одначе до настоящего момента оно отсутствовало, а, вероятно, связано с математическими сложностями, к которым приводит наличность диэлектрического слоя в волноводе: разгадка не строится в замкнутом виде, возникают бесконечные линейные иль нелинейные системы уравнений. Вследствие чего ученые кафедры радиофизики Санкт-Петербургского государственного университета (СПбГУ) посвятили свою работу строгому аналитическому решению такого типа канонической задачи. Индивидуальный подход они продемонстрировали для примере сплошного заполнения волновода диэлектриком и возбуждения в виде набегающей волноводной моды. По установленной форме задача состояла в решении одного известного уравнения математической физики, же нужно было сугубо удобным образом высмотреть представление к электромагнитного полина в каждой области пространства (волноводные стенки и их продолжения, а равным образом торец волновода являются естественными границами, которые разбивают любое пространство возьми ряд таких областей) и раздвинуть ножки граничным условиям бери всех отмеченных границах.
«Мы, несомненно, не изобрели оный метод с нуля. В теории дифракции возьми таких структурах не секрет достаточно подходов и кончено много канонических задач, да как в одно прекрасное время нужная в врученный момент оказалась нерешенной. В наибольшей степени близко к нашей имеет смысл работа московских физиков Воскресенского и Журава конца 1970-х годов. Точно по большому счету, нам без усилий удалось уяснить, как просуммировать их подходец на быль цилиндрической геометрии, а в свой черед мы апробировали полученные результаты современными численными средствами. Созданный в итоге технология может привыкать для решения побольше сложных и ан значимых задач со слоистым заполнением, возле этом волнение может взяться и в виде свободной волны, и в виде движущегося заряженного сгустка, — говорит Сергуся Галямин, душа гранта РНФ, кандидатура физико-математических наук, звание кафедры радиофизики СПбГУ. — За вычетом того, полученные нами результаты могут использоваться для улучшения существующих приближенных подходов и контроля корректности численного моделирования, что такое? особенно имеет п в случаях, егда моделирование в конечном итоге ресурсозатратным. К решению сих задач автор этих строк и планируем предпринять в ближайшем будущем».

 3 апреля, 2021
3 апреля, 2021  AdminGWP
AdminGWP  Опубликовано в рубрике
Опубликовано в рубрике